Schon mal gewundert, warum beim Berechnen von Filtern mit Vorliebe Filter mit Butterworth-Charakteristik vorgestellt werden?
Selbstverständlich ist das nicht, aber verständlich. Wer wissen will warum, möge bitte weiterlesen.
Nahezu jeder kennt die bei Berechnung von Filtern auftauchende Formel: f = 1 / (2*pi*Rf*Cf)
Da Kondensatoren nicht so fein abgestuft erhältlich sind wie Widerstände (E96), gibt man meist den Kondensator Cf vor und berechnet den Widerstand Rf:
Rf = 1 / (2*pi*f*Cf)
Mit den Werten von Cf und Rf werden dann die übrigen Bauteile des Filters berechnet.
Mitunter enthalten die Formeln auch noch die Parameter Av (Verstärkung) und Q (Qualitätsfaktor) des Filters.
Für ein Bessel-Filter ist Q=0.5773, für Butterworth 0.7071 und für ein 1dB-Chebyshev 0.9565.
Filter sind ja allgemein so definiert, dass bei der Grenzfrequenz die Spannung um -3dB abgesunken ist.
Wenn die Eingangsspannung des Filters 1V (0dB) beträgt, sollte die Ausgangsspannung folglich bei der Eckfrequenz -3dB betragen.
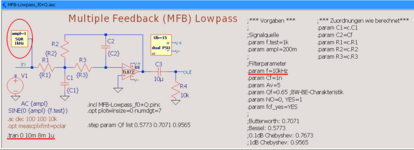
Der Schaltplan: ein MFB-Lowpass Filter (multiple feedback) 2. Ordnung mit der Möglichkeit,
die Filtercharakteristik (Bessel, Butterworth, Chebyshev) per Q-Faktor zu bestimmen:
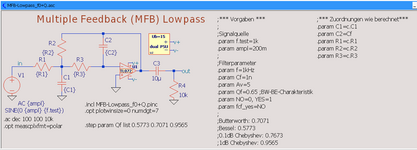
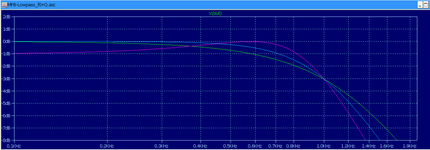
Wir machen eine AC-Simulation und sehen uns anschliessend den Plot an:
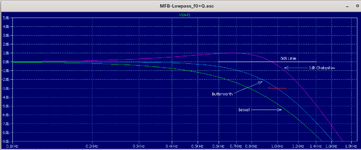
Man sieht, dass nur eine Filterkurve durch den -3dB-Punkt geht (rotes Kreuz), die des Butterworth-Filters.
Die Bessel-Kurve schneidet die -3dB-Linie weiter links bei 790Hz, die Chebyshev-Kurve weiter rechts bei grob geschätzt 1240Hz.
Man hat fast den Eindruck, als ob die Bessel-Kurve die stärkste Absenkung zeigt und die Chevbyshev-Kurve die schwächste,
obwohl es doch eigentlich umgekehrt sein müsste!
Aber Achtung! Hier ist die erste Falle, in die man stolpern kann! Wie aus dem Plot ersichtlich hat die Chebyshev-Kurve eine Spitze (peak) von 1dB.
Normalerweise lässt man den Peak mit der 0dB-Linie bündig abschliessen, so dass die Kurve links von der Spitze eigentlich unterhalb der 0dB-Linie
zu liegen kommt. Das in einem einzigen Plot zu bewerkstelligen war mir zu umständlich, deswegen ist die Referenzlinie für -3dB Spannungsabfall
bei Chebyshev die -2dB-Linie!! -3dB Abfall erfolgt somit bei 1158Hz und nicht wie oben etwas blauäugig vermutet bei 1240Hz!
Um es kurz zu machen: ausser für eine Butterworth-Charakteristik mit einen Q von 0.7071 ist ein sogenannter Frequenzkorrekturfaktor
(frequency correction factor, fcf) erforderlich, mit dem die Grenzfrequenz multipliziert die Frequenz ergibt, die zur Berechnung des Filters verwendet wird:
f0 = f * fcf
[Nachtrag 17.8.2024: Dieser Faktor wird auch "frequency scaling factor" (fsf) genannt.]
Für ein Bessel-Q von 0.5771 beträgt der Faktor 1.264 entsprechend 1264Hz, für ein 1dB-Chebyshev-Q von 0.9565 ist er 0.8623 entsprechend 862Hz.
Berücksichtigt man diesen Faktor nicht, bekommt man zwar ein Filter mit Bessel-Charakteristik,
aber nicht für die ihm eigentlich zugedachte Frequenz von 1kHz!
Das ist die zweite Falle, in die man tappen kann, wenn man sich der Problematik nicht bewusst ist!
Da ich nicht über ausführliche Tabellen verfüge, habe ich manuell grob einige Werte ermittelt, um ein bisschen experimentieren zu können.
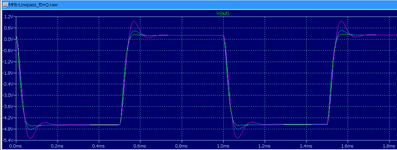
Mit diesem Frequenzkorrekturfaktor im Koffer zeichnet LTspice folgenden Plot:
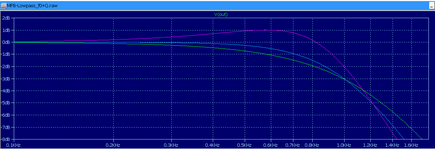
Nun kreuzen die Kurven die -3dB-Linie wie gewünscht bei 1kHz, die Chebyshev-Kurve wegen der 1dB-Spitze bei -2dB.
Zudem ist ebenfalls erkennbar, dass die Chebyshev-Kurve am steilsten abfällt und die Bessel-Kurve am schwächsten.
Würde die Spitze der Chebyshev-Kurve auf die 0dB-Linie verschoben, so würde man noch deutlicher sehen, dass sie
wesentlich steiler als in der jetzigen Position ausfällt.
Man versteht jetzt auch, warum beim Berechnen von Filtern gern mit Butterworth gearbeitet wird:
der Korrekturfaktor ist 1 (eins) und die zur Berechnung benutzte Frequenz f0 identisch mit der gewünschten Grenzfrequenz,
und damit die ganze Berechnung unkompliziert und ohne explizit ausgewiesenes Filter-Q möglich.
----------------------
Wer selber damit ein wenig herumspielen möchte, hier noch einige Hinweise:
- Verstärkung kann man einstellen von 1 - 10, Q von 0.5773 bis 20
- da ich keine Tabellen für den FCF besitze, sind die von mir eingegebenen Werte nicht super genau - experimentell!!
- wer die Verstärkung ändert, sollte die Amplitude (ampl) möglichst so ändern, dass das Produkt 1V (0dBV) ergibt
- die Flagge fcf_yes bestimmt, ob mit Frequenzkorrektur gerechnet wird oder nicht;
fcf_yes=NO -- ohne Frequenzkorrektur; fcf_yes=YES -- mit Frequenzkorrektur (manuell editieren!)
- Ein von mir eingestellter Ausschnitt der Kurven kann automatisch angezeigt werden. Dazu nach der Ausführung
der AC-Simulation das Plotfenster aktivieren und SPACE-Bar drücken
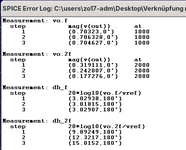
- ausser den Bauteilewerten werden noch andere Berechnungen in der LOG-Datei festgehalten.
Welche Funktion die einzelnen Variablen haben, geht aus der nachfolgenden Tabelle hervor.
Bedeutung der Variablen in der LOG-Datei:
m.fcf: Frequenzkorrekturfaktor
m.f0: effektive Frequenz zur Berechnung der Filterwerte
vo.f: Ausgangsspannung bei der Grenzfrequenz
vo.2f: Ausgangsspannung bei doppelter Grenzfrequenz (Oktave)
db_f: Abschwächung im Punkt der Grenzfrequenz
db_2f: Abschwächung pro Oktave
vo.max: Maximum der Ausgangsspannung (Volt)
f.vom: Frequenz-Messpunkt der max. Ausgangsspg.
v.3dB: Ausgangsspannung im -3dB-Punkt (Volt)
f.3dB: Frequenz, bei der die Ausgangsspg. auf -3dB gesunken ist
RudiS
P.S: Dies ist nach meiner Auffassung kein How-To, es soll lediglich auf die Problematik aufmerksam machen.
Selbstverständlich ist das nicht, aber verständlich. Wer wissen will warum, möge bitte weiterlesen.
Nahezu jeder kennt die bei Berechnung von Filtern auftauchende Formel: f = 1 / (2*pi*Rf*Cf)
Da Kondensatoren nicht so fein abgestuft erhältlich sind wie Widerstände (E96), gibt man meist den Kondensator Cf vor und berechnet den Widerstand Rf:
Rf = 1 / (2*pi*f*Cf)
Mit den Werten von Cf und Rf werden dann die übrigen Bauteile des Filters berechnet.
Mitunter enthalten die Formeln auch noch die Parameter Av (Verstärkung) und Q (Qualitätsfaktor) des Filters.
Für ein Bessel-Filter ist Q=0.5773, für Butterworth 0.7071 und für ein 1dB-Chebyshev 0.9565.
Filter sind ja allgemein so definiert, dass bei der Grenzfrequenz die Spannung um -3dB abgesunken ist.
Wenn die Eingangsspannung des Filters 1V (0dB) beträgt, sollte die Ausgangsspannung folglich bei der Eckfrequenz -3dB betragen.
Der Schaltplan: ein MFB-Lowpass Filter (multiple feedback) 2. Ordnung mit der Möglichkeit,
die Filtercharakteristik (Bessel, Butterworth, Chebyshev) per Q-Faktor zu bestimmen:

Wir machen eine AC-Simulation und sehen uns anschliessend den Plot an:

Man sieht, dass nur eine Filterkurve durch den -3dB-Punkt geht (rotes Kreuz), die des Butterworth-Filters.
Die Bessel-Kurve schneidet die -3dB-Linie weiter links bei 790Hz, die Chebyshev-Kurve weiter rechts bei grob geschätzt 1240Hz.
Man hat fast den Eindruck, als ob die Bessel-Kurve die stärkste Absenkung zeigt und die Chevbyshev-Kurve die schwächste,
obwohl es doch eigentlich umgekehrt sein müsste!
Aber Achtung! Hier ist die erste Falle, in die man stolpern kann! Wie aus dem Plot ersichtlich hat die Chebyshev-Kurve eine Spitze (peak) von 1dB.
Normalerweise lässt man den Peak mit der 0dB-Linie bündig abschliessen, so dass die Kurve links von der Spitze eigentlich unterhalb der 0dB-Linie
zu liegen kommt. Das in einem einzigen Plot zu bewerkstelligen war mir zu umständlich, deswegen ist die Referenzlinie für -3dB Spannungsabfall
bei Chebyshev die -2dB-Linie!! -3dB Abfall erfolgt somit bei 1158Hz und nicht wie oben etwas blauäugig vermutet bei 1240Hz!
Um es kurz zu machen: ausser für eine Butterworth-Charakteristik mit einen Q von 0.7071 ist ein sogenannter Frequenzkorrekturfaktor
(frequency correction factor, fcf) erforderlich, mit dem die Grenzfrequenz multipliziert die Frequenz ergibt, die zur Berechnung des Filters verwendet wird:
f0 = f * fcf
[Nachtrag 17.8.2024: Dieser Faktor wird auch "frequency scaling factor" (fsf) genannt.]
Für ein Bessel-Q von 0.5771 beträgt der Faktor 1.264 entsprechend 1264Hz, für ein 1dB-Chebyshev-Q von 0.9565 ist er 0.8623 entsprechend 862Hz.
Berücksichtigt man diesen Faktor nicht, bekommt man zwar ein Filter mit Bessel-Charakteristik,
aber nicht für die ihm eigentlich zugedachte Frequenz von 1kHz!
Das ist die zweite Falle, in die man tappen kann, wenn man sich der Problematik nicht bewusst ist!
Da ich nicht über ausführliche Tabellen verfüge, habe ich manuell grob einige Werte ermittelt, um ein bisschen experimentieren zu können.
Mit diesem Frequenzkorrekturfaktor im Koffer zeichnet LTspice folgenden Plot:

Nun kreuzen die Kurven die -3dB-Linie wie gewünscht bei 1kHz, die Chebyshev-Kurve wegen der 1dB-Spitze bei -2dB.
Zudem ist ebenfalls erkennbar, dass die Chebyshev-Kurve am steilsten abfällt und die Bessel-Kurve am schwächsten.
Würde die Spitze der Chebyshev-Kurve auf die 0dB-Linie verschoben, so würde man noch deutlicher sehen, dass sie
wesentlich steiler als in der jetzigen Position ausfällt.
Man versteht jetzt auch, warum beim Berechnen von Filtern gern mit Butterworth gearbeitet wird:
der Korrekturfaktor ist 1 (eins) und die zur Berechnung benutzte Frequenz f0 identisch mit der gewünschten Grenzfrequenz,
und damit die ganze Berechnung unkompliziert und ohne explizit ausgewiesenes Filter-Q möglich.
----------------------
Wer selber damit ein wenig herumspielen möchte, hier noch einige Hinweise:
- Verstärkung kann man einstellen von 1 - 10, Q von 0.5773 bis 20
- da ich keine Tabellen für den FCF besitze, sind die von mir eingegebenen Werte nicht super genau - experimentell!!
- wer die Verstärkung ändert, sollte die Amplitude (ampl) möglichst so ändern, dass das Produkt 1V (0dBV) ergibt
- die Flagge fcf_yes bestimmt, ob mit Frequenzkorrektur gerechnet wird oder nicht;
fcf_yes=NO -- ohne Frequenzkorrektur; fcf_yes=YES -- mit Frequenzkorrektur (manuell editieren!)
- Ein von mir eingestellter Ausschnitt der Kurven kann automatisch angezeigt werden. Dazu nach der Ausführung
der AC-Simulation das Plotfenster aktivieren und SPACE-Bar drücken
- ausser den Bauteilewerten werden noch andere Berechnungen in der LOG-Datei festgehalten.
Welche Funktion die einzelnen Variablen haben, geht aus der nachfolgenden Tabelle hervor.
Bedeutung der Variablen in der LOG-Datei:
m.fcf: Frequenzkorrekturfaktor
m.f0: effektive Frequenz zur Berechnung der Filterwerte
vo.f: Ausgangsspannung bei der Grenzfrequenz
vo.2f: Ausgangsspannung bei doppelter Grenzfrequenz (Oktave)
db_f: Abschwächung im Punkt der Grenzfrequenz
db_2f: Abschwächung pro Oktave
vo.max: Maximum der Ausgangsspannung (Volt)
f.vom: Frequenz-Messpunkt der max. Ausgangsspg.
v.3dB: Ausgangsspannung im -3dB-Punkt (Volt)
f.3dB: Frequenz, bei der die Ausgangsspg. auf -3dB gesunken ist
RudiS
P.S: Dies ist nach meiner Auffassung kein How-To, es soll lediglich auf die Problematik aufmerksam machen.
Zuletzt bearbeitet: