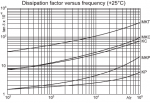
Ich möchte gerne die reale Thermische Belastung eines WIMA FKP 0,47 µF zwischen 100 und 200 kHz simulieren.
Das einfachste Ersatzschaltbild nimmt dafür einen Serienwiderstand - also ein RC-Glied.
Klingt einfach.
Nur scheint der korrekte Serienwiderstand bei bestimmten Bauformen stark frequenzabhängig zu sein.
Wima gibt an:
"Dissipation factors at +20+ C: " tan delta": 5e-4 at 1 kHz, 6e-4 @ 10 kHz, 10e-4 @ 100 kHz"
d.h. über 2 Frequenzdekaden ist dieser Faktor "annähernd" konstant.
Nur sollte er das nicht:
"tan delta" ist der Phasenwinkel der Impedanz im RC-Ersatzschaltbild.
Und nachdem der Spannungsfall an C und an R unterschiedlichen Ferquenzgang haben, sollte "tan delta" proportional zur Frequenz steigen.
tan delta = 1 / (omega * R * C)
mehrfach gegen gecheckt u.a. z.B. hier Dielektrischer Verlustfaktor – Lexikon der Kunststoffprüfung
Das tut er auch in den Simulationen einfacher RC Glieder - aber nach WIMA-Datenblatt sollte er über 2 Dekaden annähernd konstant bleiben.
Oder umgekehrt der ESP-Widerstand im Ersatzschaltbild fallen.
Ich hab verschieden Krücken versucht
OK, ich müßte vielleich alte Mathematik wieder ausgraben.
Aber ich kann mir nicht vorstellen, daß diese simple Aufgabe so kompliziert werden soll.
Und das es noch keiner gemacht hat. Kondensatoren sind jetzt keine ungewöhnlichen Bauteile...
Irgendwie fühlt es sich nach einem massiven Denkfehler an.
Hintergund:
Ich möchte einen Resonanzwandler mit 5 kW bei 50 Volt aufbauen.
Aktuell bin ich bei 45 Stück von diesen Kondensatoren parallel. Machbar, unhübsch, Streuinduktivität....
Ich krieg die höheren Ströme bei niedrigeren Frequenzen, aber alles recht nichtlinear.
Deswegen würde ich das Verhältnis Verlustleistung - Frequenz gerne genauer modellieren.
Das einfachste Ersatzschaltbild nimmt dafür einen Serienwiderstand - also ein RC-Glied.
Klingt einfach.
Nur scheint der korrekte Serienwiderstand bei bestimmten Bauformen stark frequenzabhängig zu sein.
Wima gibt an:
"Dissipation factors at +20+ C: " tan delta": 5e-4 at 1 kHz, 6e-4 @ 10 kHz, 10e-4 @ 100 kHz"
d.h. über 2 Frequenzdekaden ist dieser Faktor "annähernd" konstant.
Nur sollte er das nicht:
"tan delta" ist der Phasenwinkel der Impedanz im RC-Ersatzschaltbild.
Und nachdem der Spannungsfall an C und an R unterschiedlichen Ferquenzgang haben, sollte "tan delta" proportional zur Frequenz steigen.
tan delta = 1 / (omega * R * C)
mehrfach gegen gecheckt u.a. z.B. hier Dielektrischer Verlustfaktor – Lexikon der Kunststoffprüfung
Das tut er auch in den Simulationen einfacher RC Glieder - aber nach WIMA-Datenblatt sollte er über 2 Dekaden annähernd konstant bleiben.
Oder umgekehrt der ESP-Widerstand im Ersatzschaltbild fallen.
Ich hab verschieden Krücken versucht
- resonante LC-Komponenten
- Kaskaden von parallelen RC-Gleidern, ca 3...4 / Frequenzdekade
- einen Trafo über C mit einem Verlustwiderstand
- (noch nicht probiert) behavioural Capacity, nur wie komm ich an die Frequenz? In der AC-Anlayse OK, aber im .transient?
OK, ich müßte vielleich alte Mathematik wieder ausgraben.
Aber ich kann mir nicht vorstellen, daß diese simple Aufgabe so kompliziert werden soll.
Und das es noch keiner gemacht hat. Kondensatoren sind jetzt keine ungewöhnlichen Bauteile...
Irgendwie fühlt es sich nach einem massiven Denkfehler an.
Hintergund:
Ich möchte einen Resonanzwandler mit 5 kW bei 50 Volt aufbauen.
Aktuell bin ich bei 45 Stück von diesen Kondensatoren parallel. Machbar, unhübsch, Streuinduktivität....
Ich krieg die höheren Ströme bei niedrigeren Frequenzen, aber alles recht nichtlinear.
Deswegen würde ich das Verhältnis Verlustleistung - Frequenz gerne genauer modellieren.