Wie oft habe ich mir vorgestellt, wie schön es doch wäre, wenn LTspice über eine Scripting-Sprache verfügen würde!
Es hat mich umso mehr gereizt, mal etwas eher Mathematisches in LTSpice zu versuchen.
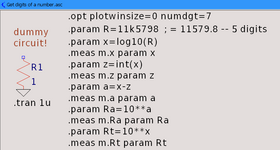
Das Ergebnis ist eine Funktion (eher ein paar Funktionen), die zu einem (nahezu) beliebigen Widerstand >=10 Ohm, <=100 MegOhm den nächstliegendsten E12-Normwert berechnet.
Dieser kleine Beitrag stellt auch eine Ergänzung zu meinem Howto Kleine Einführung zu benutzerdefinierten Funktionen dar.
Ich habe das Ganze nicht ausführlich getestet, aber es scheint soweit ok zu sein.
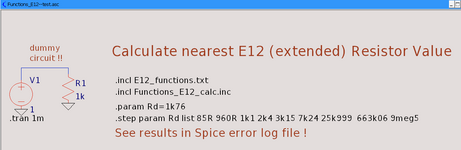
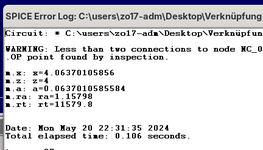
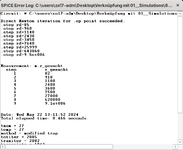
Das Ergebnis kann man in der Spice error log einsehen:
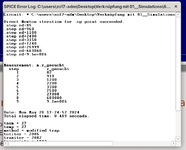
Die für die Simulation erforderlichen Dateien befinden sich - wie immer - im beigefügten Archiv.
Über Rückmeldungen würde ich mich freuen.
RudiS
Wer genauer wissen möchte, wie das Ganze func-tioniert, sollte die weiter unten mit Spicer geführten Dialoge und Erläuterungen
studieren!
Nachtrag 22.Mai:
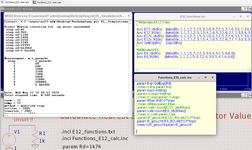
Ich hatte in der Datei "Functions_E12_calc.inc" den Exponenten der Zehnerpotenz dummerweise "idx" benannt, das kann leicht verwechselt und missverstanden werden.
Da "exp" in LTspice schon mit der e-Funktion belegt ist, habe ich "idx" in "expo" umbenannt und das Archiv dementsprechend geändert. Diejenigen, die vor dem 22. Mai
das Archiv runtergeladen haben, bitte ich um Nachsicht.
Nachtrag 26. Mai:
Ich habe die E-Funktionen um einen Wert am Ende erweitert. Normalerweise ist der Endwert bei E12 8k2, bei der von mir erweiterten E12X 9k1.
Wenn jetzt der gesuchte Wert 9k75 wäre, würde in der alten Form 8k2 bzw. 9k1 als nächstliegenster Wert ausgegeben, obwohl der Wert 10k als Normwert
viel näher liegt. Ich habe daher die Reihe um diesen neuen Endwert ergänzt. Das Archiv lasse ich erst einmal so wie es ist,
hänge aber die neue Datei "E12_functions.txt" hier an.
Es hat mich umso mehr gereizt, mal etwas eher Mathematisches in LTSpice zu versuchen.
Das Ergebnis ist eine Funktion (eher ein paar Funktionen), die zu einem (nahezu) beliebigen Widerstand >=10 Ohm, <=100 MegOhm den nächstliegendsten E12-Normwert berechnet.
Dieser kleine Beitrag stellt auch eine Ergänzung zu meinem Howto Kleine Einführung zu benutzerdefinierten Funktionen dar.
Ich habe das Ganze nicht ausführlich getestet, aber es scheint soweit ok zu sein.

Das Ergebnis kann man in der Spice error log einsehen:

Die für die Simulation erforderlichen Dateien befinden sich - wie immer - im beigefügten Archiv.
Über Rückmeldungen würde ich mich freuen.
RudiS
Wer genauer wissen möchte, wie das Ganze func-tioniert, sollte die weiter unten mit Spicer geführten Dialoge und Erläuterungen
studieren!
Nachtrag 22.Mai:
Ich hatte in der Datei "Functions_E12_calc.inc" den Exponenten der Zehnerpotenz dummerweise "idx" benannt, das kann leicht verwechselt und missverstanden werden.
Da "exp" in LTspice schon mit der e-Funktion belegt ist, habe ich "idx" in "expo" umbenannt und das Archiv dementsprechend geändert. Diejenigen, die vor dem 22. Mai
das Archiv runtergeladen haben, bitte ich um Nachsicht.
Nachtrag 26. Mai:
Ich habe die E-Funktionen um einen Wert am Ende erweitert. Normalerweise ist der Endwert bei E12 8k2, bei der von mir erweiterten E12X 9k1.
Wenn jetzt der gesuchte Wert 9k75 wäre, würde in der alten Form 8k2 bzw. 9k1 als nächstliegenster Wert ausgegeben, obwohl der Wert 10k als Normwert
viel näher liegt. Ich habe daher die Reihe um diesen neuen Endwert ergänzt. Das Archiv lasse ich erst einmal so wie es ist,
hänge aber die neue Datei "E12_functions.txt" hier an.
Anhänge
Zuletzt bearbeitet: